Testing superscripts

(a + b)² = a² + 2ab + b²

old school programmer

Answers to homework #10

When F = 40, C = 5/9(40-32) = 5/9(8) = 4.44 degrees

When F = 60, C = 5/9(60-32) = 5/9(28) = 15.56 degrees

When C = 30, F = 9/5(30) + 32 = 9*6 + 32 = 54 + 32 = 86 degrees

When C = 40, F = 9/5(40) + 32 = 9*8 + 32 = 72 + 32 = 104 degrees

Find where y = 7x + 4 and y = 10x - 5 intersect.

Step 1: Set the equations equal to each other and solve for x.

7x + 4 = 10x - 5_____Subtract 7x from both sides.

4 = 3x - 5_________Add 5 to both sides.

9 = 3x___________Divide both sides by 3.

3 = x

Step 2: Plug x=3 into either equation to find y.

y = 7(3) + 4 = 25

The point of intersection is (3, 25).


Kramer's rule problems.

3x + 4y = 25
4x - 2y = 4

Matrix version
[3 _4 | 25]
[4 -2 | _4]

Three matrices.

M
[3 _4 ]
[4 -2 ]

determinant = 3x(-2) - 4x4 = -6 - 16 = -22

Mx
[25 _4 ]
[ 4 -2 ]

determinant = 25x(-2) - 4x4 = -50 - 16 = -66

My
[3 _25 ]
[4 __4 ]

determinant = 3x(4) - 4x25 = 12 - 100 = -88

x = -66/-22 = 3
y = -88/-22 = 4

Answer: (3, 4)

2x + 4y = 10
4x + 8y = 30

Matrix version
[2 4 | 10]
[4 8 | 30]

Three matrices.

M
[2 4 ]
[4 8 ]

determinant = 2x8 - 4x4 = 16 - 16 = 0. This means no single solution.

Mx
[10 4 ]
[30 8 ]

determinant = 10x8 - 30x4 = 80 - 120 = -40. Since this isn't 0, the two lines are parallel.

We don't have to do the third determinant. Yay!

Answer: No solution, two parallel lines.

_x + _y = 13
3x - 3y = 9

Matrix version
[1 _1 | 13]
[3 -3 | _9]

Three matrices.

M
[1 _1 ]
[3 -3 ]

determinant = 1x(-3) - 3x1 = -3 - 3 = -6

Mx
[13 1 ]
[ 9 -3 ]

determinant = 13x(-3) - 9x1 = -39 - 9 = -48

My
[1 _13 ]
[3 __9 ]

determinant = 1x9 - 3x13 = 9 - 39 = -30

x = -48/-6 = 8
y = -30/-6 = 5

Answer: (8, 5)

Final homework not accepted late.

The last homework is due tomorrow. I will post the correct answers after class so students can study from them. I will not accept the assignment after end of class tomorrow

practice for slope and slope intercept from point slope

1a) Find the slope of the line that passes through (1, 5) and (4, -7).
1b) Find the slope intercept version of the linear equation for this line.

2a) Find the slope of the line that passes through (1, 0) and (4, 0).
2b) Find the slope intercept version of the linear equation for this line.

3a) Find the slope of the line that passes through (1, 4) and (1, -7).
3b) Find the slope intercept version of the linear equation for this line.

Answers in the comments.

practice for triangles, angles and sides

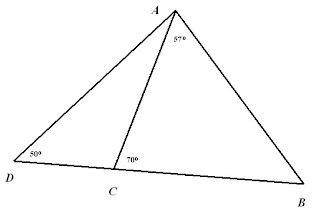In this picture, we are told the measure of three angles. This is enough information to find the measure of all the angles.

1) Find the measure of angles DCA, DAC and CBA.

There is also a rule in a triangle that if one angle is larger than another, the opposite side of the big angle must be longer than the opposite side of the smaller angle.

2) Use the rule to put this list of line segments in order from longest to shortest. AB, AC, AD, BC, CD.

Answers in the comments.

Classifying triangles

There are two ways to classify triangles. The first way deals with the size of the largest angle in the triangle.

Obtuse triangle: A triangle is obtuse if the largest angle is greater than 90 degrees in measure. If the sides are given as a, b and c, where c is the longest side, if a^2 + b^2 < c^2, the triangle is obtuse.

Right triangle: If the largest angle is exactly 90 degrees in measure, the triangle is a right triangle. If the sides are given as a, b and c, where c is the longest side, a^2 + b^2 = c^2 means we have a right triangle. This is known as the Pythagorean Theorem.

Acute triangle: If the largest angle is less than 90 degrees, the triangle is called an acute triangle. If the sides are given as a, b and c, where c is the longest side, a^2 + b^2 > c^2 means we have an acute triangle.

The other method of classification has to do with having angles of the same measure or sides of the same length.

Equilateral triangle: All three angles have the same measure, 60 degrees. All three sides are the same length.

Isosceles triangle: At least two sides have the same measure, which also means two angles must have the same measure. Technically, and equilateral triangle is still isosceles, but it is a special case and we usually name it by the more specific name.

Scalene triangle: All three sides are different lengths, and all three angles are different measure.


Practice problems.

1) Can a triangle be both a right triangle and an isosceles triangle?

2) A triangle has side lengths 3, 3 and 4. What are its two classifications?

3) A triangle has two angles, 70 degrees and 15 degrees. What are its two classifications?

4) An isosceles triangle has one angle of measure 40 degrees. What are the two possible sets of angle measures and classify both as acute, right or obtuse.

5) A triangle has side lengths 5, 12 and 13. What are its two classifications?

Answers in the comments.

practice problems for truth tables

Instead of columns running left to right, it's easier in this text editor to make a truth table that is put together in rows going from top to bottom

Here is an example: Create the truth table for (p OR q) IMPLIES q.

p__________________ T T F F
q__________________ T F T F
p OR q_____________ T T T F
(p OR q) IMPLIES q_ T F T T

Not a tautology, because of the F in the second position.

Try the following.

a) (p IMPLIES q) OR (p IMPLIES NOT q)

b) (NOT p) IMPLIES (p IMPLIES q)

Answers in the comments.

practice for bitwise operators

p = 1001 1010
q = 0110 0110
r = 1011 0001

^ means and
v means or
~ means not

Order of operations: parentheses first, otherwise left to right

Find the following values.

a) p v q
b) p ^ r
c) p v ~q
d) ~p v q
e) r ^ ~q
f) ~(r ^ q)

Answers in the comments.

Five computer scientists

Here are the highlights of the life stories of five important people in the history of computer science. There are many others, but these folks made significant contributions and their lives have interesting and unique tidbits which will be shared here.



Born Janos Von Neumann in Hungary, he is known to posterity as John Von Neumann, though his friends always called him Johnny.

I give Von Neumann the first position on this list because he is the greatest mathematician on the list. The list of four great mathematicians I lectured about on the first day only takes us through to 1855, when Gauss dies. If we were listing great mathematicians since then, almost all mathematicians would put Bernhard Riemann, Henri Poincaré, David Hilbert and John Von Neumann on the list of the greatest of the great.

Not Albert Einstein. He is a great physicist, but not a great mathematician.

Von Neumann started his career in chemistry, but after he did the mathematical groundwork for the ideas of quantum mechanics, he switched to mathematics. This is some of the strangest and least intuitive mathematics ever done, and it shows that at the sub-atomic level, it is possible for some small objects to be in two places at the same time. When people would ask him how he understood some of the strange ideas he came up with in his life, Von Neumann said: "You don't really ever understand higher mathematics. You just get used to it."

Besides his work in mathematical physics, Von Neumann solved a conjecture of Borel and created the field now known as game theory. A century before, a Prussian tactician named Von Clausewitz put forward the idea of total war, that a country at war must put forward every available resource or it wasn't truly war at all. Von Neumann's game theory proved Von Clausewitz wrong, that successful war strategies include bluffs and strategic ways to put forward only part of the available resources and still meet your objectives.

Among his practical inventions include the trigger for the hydrogen bomb, which makes an atomic explosion "slow" enough that it begins a larger chain reaction instead of obliterating all matter in a radius of several hundred yards instantly. The larger chain reaction makes for an explosion thousands to millions of times stronger.

The reason Von Neumann is on this list is because he invented the idea of software. When the first computer were created, they had to be re-wired by hand every time a new problem was to be solved. There was computer memory, but it just stored data. Von Neumann put forward the idea that some of the memory hold instructions, and the computer should be hard-wired to understand these instructions. It is nearly impossible to overestimate the importance of this idea.

Von Neumann died of cancer in 1957 at the age of 53. The amount of important work he did in such a short life is as amazing as any of the great composers who died young, like Mozart or Chopin.



Alan Turing was born in England, and he was an excellent math student before the innovation of computers. He is given credit as one of the people who proved the Central Limit Theorem, a key fact that makes statistics work.

Turing's most famous practical work was breaking the German codes during World War II using some of the first computers ever built. The Germans had a code machine called Enigma, which could scramble a message in a way that was very difficult to unscramble without another Enigma machine at the other end AND the particular starting position of the machine when the operator began typing the message in. The British code breaking team was housed during the war at Bletchley Park, and some of the things that happened there have only been de-classified in the past ten years of so. All the information points to Turing as being the intellectual star of the team.

Turing also came up with theoretical concepts in early computers, including the Turing machine, an idealized computer with two tapes, one for input and one for output, and the Turing test for artificial intelligence.

Turing was also very openly gay at a time when that was illegal. He was charged in a court of law with engaging in homosexual acts and found guilty. He was given the option of going to jail or taking a "cure" of estrogen treatments. He chose the cure. It did nothing to change his feelings, but it did make his breasts bigger.

Turing died in 1954 at the age of 41 from eating a poison apple. He was working on electrolysis, a way of plating one metal on top of another, in this case silver plating, and absent-mindedly picked up an apple and took a bite when his hands were covered with poisonous chemicals. The authorities ruled it a suicide, though Turing's mother believed it was just an accident.



Back in the day, the actual work of programming was considered "woman's work", and many of the programmers back in the era of the huge mainframes were women, who were considered better suited to the painstaking work of making sure there were no errors in a piece of computer code. This stereotype made it possible for some women to get employment other than secretarial work in business in the middle of the century in the United States, and the stereotype continued in Japan well into the 1980's, when I was a programmer of video games in the U.S. In the era of Pac-Man and Donkey Kong, the video game designers in Japan were men, but the programmers were women.

Grace Hopper was born in New York City in 1906. She was a good math student, getting her bachelor's degree from Vassar and her doctorate at Yale. During World War II, she worked for the Navy and was on the team creating some of the first computers used by the U.S. Military, including the Mark I.

She is given credit for finding the first computer bug, which means a mistake in the program which keeps it from running properly. The bug she found was an actual bug, a moth that found its way into the computer and died when it hit the exposed wires, causing a short circuit.

Her ideas about designing a software language gave rise to COBOL, a language that was the standard for business software for many decades. Though it has been eclipsed by more modern languages, there are still listings for jobs for people who program in COBOL to this day.

She wanted to understand the connection between the speed of light and the workings of the computer that work on electricity, which moves at very close to the speed of light, so she had engineers cut pieces of wire that would show how far electricity would travel in a nanosecond, a billionth of a second, and she would hand these wires out when she gave lectures.

Hopper kept her Navy commission throughout her life, and retired with the rank of Rear Admiral.

She died in 1992 at the age of 85. She was buried with full military honors at Arlington National Cemetery. The U.S.S Hopper is one of the few ships in the Navy named after a woman, and the ship has the same nickname that the admiral had in life, Amazing Grace.


Edsger Dijkstra was born in Holland in 1930, about a generation after Hopper and Turing and Von Neumann, and his contributions to computer science dealt with changing computer programming from a haphazard practice to a well-structured and defined set of proper practices.

He started working in computers in the 1950's, and computers were still strange and exotic devices to the general public. When Dijkstra applied for his wedding license, her put "computer programmer" down as his line of work. The clerk at the registrar's office made him change it, saying that nobody programmed computers for a living. He crossed it out and wrote "theoretical physicist", which the registrar accepted as a real job people get paid for.

While Dijkstra is given credit for developing some important methods for solving problems, his main influence today is the idea that a computer program should be completely designed before anyone ever starts typing in code into a machine. There were some computer languages he felt caused people to fall into bad habits, including Grace Hopper's COBOL and other popular languages of the 1960's, including BASIC and FORTRAN. A more modern concept in programming called object oriented programming also met with his disapproval. "Object oriented programming is an exceptionally bad idea that could only have originated in California."

Another famous quote attributed to him is: "Computer Science is no more about computers than astronomy is about telescopes."

Dykstra died at the age of 72 in 2002. When asked by an interviewer what he would like to be remembered for, he replied: "If some day, someone is writing a computer program and is thinking about how to do a quick and sloppy job, and for a moment that person considers 'What would Dykstra make of this?', then decides to design the program carefully, that will be immortality enough for me."


Donald Knuth was born in Wisconsin in 1938. He was a very good student and at an early age he showed how obsessed he could be with solving a problem. He skipped nearly a week from high school trying to win a national competition to find the most words that could be made using the letters in the phrase "Ziegler's Giant Bar." Knuth found 2,500 words. The second place competitor found about 600. He said he could have found more if he had realized he was allowed to use the apostrophe. The prize was a television set, which he donated to the high school.

Knuth's best known work is the textbook series The Art of Computer Programming. The first four volumes have been around since the 1970s and 1980s. The fifth volume was released only a few years back. When people send Knuth corrections to his textbooks, he send the first person who correctly spots an error a check for $2.56. The number 256 is the number of different patterns an eight bit binary string can create. Most people who get the checks frame them and hang them on their walls as souvenirs.

Donald Knuth is still alive and is professor emeritus of computer science at Stanford University. A devout Lutheran, his web page lists his public speaking engagements, and includes the Sundays when he will give a sermon as the deacon of his church on some text from the Bible.

Practice for tomorrow's exam

Consider the contingency table below. The columns represent A and A-bar, the complement of A, while the rows represent B and its complement B-bar. The numbers are the number of element in each intersection.

_______________A____A-bar_____row totals
B_____________25________________75
B-bar_________________50___________
col. totals___90_____________________grand total

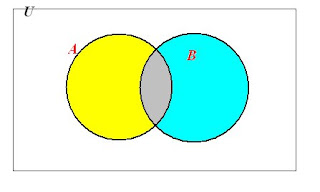Use the numbers from the filled in table to find the cardinalities in each section.

Cardinality in white section =
Cardinality in yellow section =
Cardinality in gray section =
Cardinality in cyan section =

Answers in the comments.

Practice with Polish notation

Find the values of the numbers from these expressions.

- + ^ 10 2 20 + 12 17 =

- 12 * 2 + 4 ^ 3 - 2 1 =

Turn these equations in standard notation into Polish notation.

y = ax^2 + bx + c

A = Pe^(rt)

Answers in the comments.

Practice for test 7/7

A) A rock concert registers at about 105 decibels and a jet engine at 140 decibels. How many more times the energy is produced by the engine compared to the speakers at the concert?

Use the order of operations to get a single number from these mathematical terms. If the answer is not a whole number, round to two places after the decimal.

Note: sqrt(...) means square root, / means division, ^ means exponentiation and * mean multiplication.

B) sqrt(7^2 + 1^2)

C) 8 - 4
__12-(-8)

D) 3(5+2) - 4/6*15 + 8(3/2)


Answers in the comments.

Practice problems for homework due July 6

"^" means exponentiation. "sqrt(x)" means square root of x, which can also be written as "x^(1/2)". The symbol ~= means approximately equal.

log 5 ~= .69897 and log 7 ~= .84510.
log(a*b) = log a + log b
log(a/b) = log a - log b
log a^b = b*log a
log (sqrt(a)) = 1/2*log a.

Find the following values, rounded to the nearest five decimals.

a) log 35 =

b) log (sqrt(35)) =

c) log 7/5 =

The prime factorization of 108 is 2^2 * 3^3. Find the simplified radical form of for the following radicals, and the approximations to five significant digits.

d) sqrt(108) =

e) 108^(1/3) =

f) An earthquake registering 5.7 is recorded one morning, and in the afternoon, another quake 27 times stronger is felt. Give the Richter reading of the second stronger quake. (Nearest tenth.)

g) What is the decibel reading of a sound that is 7 times louder than a 75 decibel reading. (Nearest decibel.)

Answers in the comments.

Practice problems for the test on 7/2

The Transformers sequel made $108,966,307 this weekend.

a) Round this number to one significant digit.
b) Round this number to two significant digits.
c) Round this number to three significant digits.

According to the calculator 50! rounds to 3.041 x 10^64 and 60! rounds to 8.321 x 10^81, both rounded to four significant digits. Find the following values.

d) 50! / 60!
e) 60! / 50!
f) 50! x 60!
(note: the calculator will tell you overflow error on problem f because it doesn't like numbers bigger than 10^100 power. You will have to do this one by hand.)

Answers in the comments.

Preview for 6/30

Today, the topics are going to be the metric system and the English measurement system and how to switch back and forth, and how to represent numbers using scientific notation, which is useful for really big numbers and numbers really close to zero. Scientific notation is used by calculators when there are too many digits to represent a number the regular way.

If we have time, the next topic will be logarithms.

There will be a quiz at the end of class. The topics include greatest common divisor (g.c.d.), least common multiple (l.c.m), representing numbers in decimal, hexadecimal and binary, and a basic understanding of the root words and prefixes of the metric system.

practice for tomorrow's quiz

1. Given the following death statistics, find the rate per 100,000 population. Round to the nearest whole number.

a) 1950: U.S. population = 151,000,000
number of heart disease deaths = 886,000

b) 1970: U.S. population = 203,000,000
number of heart disease deaths = 1,000,000

c) 1990: U.S. population = 249,000,000
number of heart disease deaths = 801,000

2) For the following words in metric terminology, tell whether the measure is in length, volume or weight, and how many of the main unit there is given the prefix.

Example: hectometer
length, 100 meters

a) millimeter

b) centiliter

c) metric ton

Answers in the comments.

preview for 6/29

Today, we are going to cover how to change from a repeating decimal to a fraction. We will also deal with scales using powers of 10, including percents and smaller scales, and start discussing the metric system. if we have time, we will start working with scientific notation.

Repeating decimals into fractions - page 7

Scales based on powers of 10 - pages 12 through 17

The metric system - pages 15 and 16

Scientific notation - pages 17 through 19

practice problems for changing bases

1) Change FADhex into decimal.

2) Change FADhex into binary.

3) Change 1,776dec into hexadecimal.

4) Change 1,776dec into binary.

5) Change 110 0101 0000 0110bin into hexadecimal.

6) Change 110 0101 0000 0110bin into decimal.

Answers in the comments.

Binary and Hexadecimal representation

In computers, the machine only really understands two states, on and off, which we can represent with 1 and 0. This is called a binary system, and just like the decimal system, any number can be represented in binary by using the place holder system, so instead of just one on-off switch we ca have a series of on-off switches to represent more complex concepts and larger numbers.

It's very hard for people to read long strings of 1's and 0's, so a system where four bits are put together to represent a number between 0 and 15 was created. Base 16 is called hexadecimal, and we will see how to represent numbers in this system and switch back and forth between base 10, base 2 and base 16.

In base 10, when we count the number of digits in a number, we know the approximate size of the number a 4 digit number, like 2,678 or 5,321, is between 1,000 (10x10x10) and 10,000 (10x10x10x10). We call this the order of magnitude for a number, the largest power of ten needed to represent the value. The order of magnitude of an n digit number is n-1.

In binary, the number of digits tells us the largest power of two needed to represent the value. The powers of 2 from 2^0 to 2^10 are:

2^0 = 1
2^1 = 2
2^2 = 4
2^3 = 8
2^4 = 16
2^5 = 32
2^6 = 64
2^7 = 128
2^8 = 256
2^9 = 512
2^10 = 1,024

In base 2, we only have two symbols, 0 and 1. A binary digit is called a bit, and a series of 1's and o's is called a bitstring. When a number is represented in this part of the class, we will put the suffix bin, dec or hex behind it to show if it it the binary representation, the decimal representation or the hexadecimal representation.

Changing between bases

Example: 110 1101 1110 0101bin is a number represented in binary. (It is customary to put a space between digits to split them into packets of four bits.) Here is the method to turn this into a number represented in decimal.

Take the first bit on the left and put that into a variable we will call answer. If there are still bits in the string, multiply answer by 2 and add the next bit. We strip off the bits as we go.

110 1101 1110 0101bin answer=1.
10 1101 1110 0101bin answer=1*2+1 = 3.
0 1101 1110 0101bin answer=3*2+0 = 6.
1101 1110 0101bin answer=6*2+1 = 13.
101 1110 0101bin answer=13*2+1 = 27.
01 1110 0101bin answer=27*2+0 = 54.
1 1110 0101bin answer=54*2+1 = 109.
1110 0101bin answer=109*2+1 = 219.
110 0101bin answer=219*2+1 = 439.
10 0101bin answer=439*2+1 = 879.
0 0101bin answer=879*2+0 = 1,758.
0101bin answer=1,758*2+0 = 3,516.
101bin answer=3,516*2+1 = 7,033.
01bin answer=7,033*2+0 = 14,066.
1bin answer=14,066*2+1 = 28,133.

This means 110 1101 1110 0101bin = 28,133dec, which is to say in decimal representation, the standard way we write numbers. The thing is, there are a lot of chances to make mistakes. Base 16 was developed to be a bridge between machines that understand binary language and the people who program them. Since 16 = 2^4, if we have bitstrings of length four we can make sixteen distinct patterns, which represent the numbers from 0 to 15. Here are the patterns, with the idea that each bit represents a power of 2, specifically 8, 4, 2 and 1.

8421
_______ hex (decimal)
0000 -> 0
0001 -> 1
0010 -> 2
0011 -> 3
0100 -> 4
0101 -> 5
0110 -> 6
0111 -> 7
1000 -> 8
1001 -> 9
1010 -> A (10)
1011 -> B (11)
1100 -> C (12)
1101 -> D (13)
1110 -> E (14)
1111 -> F (15)

Using this table, it's easy to switch between binary and hexadecimal and vice versa, and changing from decimal to hexadecimal and vice versa is easier that the switch directly from decimal to binary.

110 1101 1110 0101bin = 6DE5hex

Switching from hexadecimal to decimal is like the method for switching from binary to decimal, expect that you multiply the answer by 16 at each step.

6DE5hex answer = 6
DE5hex answer = 6*16+D (13) = 109
E5hex answer = 109*16+E (14) = 1,758
5hex answer = 1,758*16 + 5 = 28,133

Notice that this is exactly the same answer as before, 218,133 in decimal, but it only took us four steps instead of fifteen.

Changing from decimal to another base is a matter of dividing by that base. Again, changing to hexadecimal is easier than changing to binary because there are less steps, and if we need binary, the switch back and forth between binary and hexadecimal is easy.

7,592dec into hex.

Divide 7,592 by 16 and we get 474, remainder 8. Answer = 8hex.
Divide 474 by 16 and we get 29, remainder 10. 10 becomes A in hex. Answer = A8hex.
Divide 29 by 16 and we get 1, remainder 13. 13 becomes D in hex. Answer = DA8hex.
Since 1 is less than 16, this is the last digit in our answer. Answer = 1DA8hex.

So the answer is 1DA8 in base 16, which we pronounce "one D A eight". Words like "thousand" and "hundred" only have meaning in base 10. If we want the answer in binary, it's easy to change the hex digits into bits.

1DA8hex = 0001 1101 1010 1000bin

In a computer, the pattern might include all the bits, including the leading zeros, but we might also write the answer without the leading zeros as 1 1101 1010 1000bin.


The notes for these topics are on pages 20 to 23.

Practice problems for prime factorization

Find the prime factorizations of the following numbers.

a) 128
b) 129
c) 130

d) Find all the factors of 130.

Answers in the comments.

Representing numbers by prime factorization

I'm going to be putting previews of notes for class before the class, then fleshing in the details and possibly adding more or taking away topics from the list, depending on how far we get.


Prime numbers, composite numbers and the number 1 (unit)
prime factorization
relatively prime numbers
shortcuts for divisibility
reducing fractions
greatest common divisor (g.c.d.) and least common multiple (l.c.m.) for two numbers

These topics are covered on pages 23 through 28 in the notes.

Roman vs. Hindu-Arabic numerals, fractions vs. decimals

Roman vs Hindu-Arabic

We take our number system for granted. All around the world, if someone writes 647, it is understood to mean six hundred forty seven. We have ten digits and a placeholder system, and we can not only write any whole number, we can write negative numbers and numbers with decimal and many more variations. This system is known as the Hindu-Arabic numeral system, and it has become the worldwide standard because of its ease of use and versatility. But if we go about 500 years back in Europe, only a few educated people would know about the Hindu-Arabic system and most people would be using Roman numerals.


Roman numerals had a total of seven symbols, which were letters used in nearly every European alphabet, I, V, X, L, C, D and M, and another non-letter symbol, a bar placed over a number. The bar over letters meant to take those letters, figure out what numbers they stood form then multiply that by 1,000.

The symbols stood for numerical values, and when they were written the symbols were put in order left to right with the largest symbols first down to the smallest symbols. There were a few legal combinations where a small number symbol could be put before a big number symbol, and the rule were as follows.

Rule 1: The small number symbol must represent a power of 10, I for 1, X for 10 or C for 100.
Rule 2: The large number symbol that followed the small must be either five times larger or ten times larger. The six possible combinations are list in the picture above.

If we wanted to represent the number 642,318 in Roman numerals, we would have the symbols for 642 under a bar followed by the symbols for 318. It would look like this.

______
DCXLIICCCXVIII

Below, the symbols are put in red and black to show which groups of symbols represent which digit in the number 642,318.
______
DCXLIICCCXVIII

The rules are that if we want to represent a number in the hundreds place, we look for the first instance of a D or C. For the tens place, we look for the first instance of a L or X, and the ones place starts when we see the first instance of a I or V.

While reading and writing Roman numerals can be taught fairly easily, addition and subtraction rules are a little cumbersome, while multiplication and division are truly difficult. Because of this, Roman numerals have disappeared as a way to represent numbers except in ornamental ways, like Super Bowls and fancy clock numbers.

Fractions vs. Decimals

Fractions and decimals are two different ways to represent the same types of numbers. Both methods have advantages and disadvantages, so unlike Roman numerals, neither method is likely to go away soon.

Mathematicians like fractions because they are precise. When I write 5/13, this means the exact number that when I multiply it by 13, I get 5. If you put 5/13 in a calculator, the readout will be 0.384615385, and that's just the first nine digits after the decimal place. The true representation goes on forever, but because it is a rational number it has a pattern that repeats. The standard way to write a repeating decimal is to put a bar over the repeating part so in this instance we have

_______
.384615 = 5/13

One of the drawbacks of fractions is that if they have different denominators, it can be hard to tell which is larger. Foe example, is 5/11 larger than 4/9? It's hard to tell looking at them, but if we find a common denominator, like 11x9 = 99, it becomes clear.

(5x9)/(11x9)= 45/99
(4x11)/(9x11)=44/99

In this case 5/11 is greater than 4/9. If we went to our calculators and found the decimal representations, it would be very clear immediately.

5/11 = .45454545...
___
.45 = 5/11

4/9=.4444...
__
.4= 4/9

Since the first time the number disagree, the 5 in the hundredths place is bigger than the 4 in the hundredths place, that means 5/11 is the larger of the two numbers.

It's important to realize that any time we round a decimal number off and we lose information, we do not get a true exact value of a fraction. Some fractions terminate, but only if the denominator is only divisible by 2 or 5.

practice problems for homework 1

Change these numbers in Hindu-Arabic to Roman numerals.

631 = ______

15,781 = _____

Change these numbers in Roman numerals to Hindu-Arabic.
__
IXCDXLIV = ____

DCXCVII = ____

Find the approximation of 7/37 to the following number of decimal places and find the exact repeating decimal representation.

7/37 to the nearest tenth = _____
7/37 to the nearest hundredth = _____
7/37 to the nearest thousandth = ____

Repeating decimal representation = _____

Answers in the comments.

Four great mathematicians

Archimedes of Syracuse: born 287 BC, died 212 BC. The greatest thinker of antiquity. Known for inventions for centuries, including weapons he developed for his relative King Hieron of Syracuse and a famous method for irrigation called the Archimedes Screw, still used to this day, he was proudest of the mathematics he did, and asked for one of his discoveries, the relation between a cylinder and a sphere inscribed in it, to be put on his tomb. There are three famous stories about him that include quotes.

"Eureka!": King Hieron was given a gift of a gold crown, but he wanted to make certain it was really gold without melting it down. He asked Archimedes if he could come up with a test. Archimedes has in his bathtub when he saw the level of the water rose when he entered, and thought about why a large boat would float while a small rock would sink. He came up with the laws of displacement and realized it could be used to see if the crown was really gold or just another metal with gold plating. He was so excited by this, he ran through the streets of Syracuse to the palace of the king naked, yelling "Eureka!" which means "I have found it!"

"Give me a lever and a place to stand and I could move the earth.": Archimedes challenged a mighty warrior to move a massive stone brought to the palace. The warrior could not, but Archimedes took a long piece of wood, and using a small rock as the fulcrum, he was able to move the large weight using leverage. Many of his inventions used leverage, either directly like a lever and fulcrum or indirectly like turning screw.


"Don't disturb my circles!": The Roman general Marcellus was invading Sicily and laid siege to Syracuse. He gave specific orders that Archimedes was to be captured and brought to him alive. With the battle raging in the city, Archimedes, then in his seventies, was working hard on a geometry problem and paid no attention to the clamor around him. A soldier burst into his home and found him on his patio working on math. Archimedes did not notice the soldier until the man's shadow cast on the work Archimedes was doing, and when that happened, Archimedes spoke sharply at the young man. "Don't disturb my circles!" the old man snapped, and the soldier, unhappy with the disrespect, stabbed and killed Archimedes. Marcellus was very upset by this, and paid for lavish tomb to be built for the great inventor, with the cylinder and sphere put on top of it.

As great as his reputation has been for more than two thousand years, Archimedes had a new work "discovered" in the 20th Century, when an illuminated prayer book from the 10th Century was discovered to be a palimpsest of one of Archimedes' lost works, which is a book written over the paper of another book. This work shows that he understood the basic concepts of integral calculus, a field of study not fully understood by the rest of mankind until our next great mathematician comes along.


Sir Isaac Newton: born 1642, died 1727. Born in England prematurely on Christmas day, 1642, Newton's father was quoted as saying that Isaac could fit in a pint mug when he was born. His father died soon after and his mother re-married, and the family struggled to make ends meet. Newton's cleverness showed itself early as he designed toys for himself that actually worked, like a toy wagon whose wheels turned and whose axle could be steered. The owner of the land on which Newton's father worked decided to sponsor the boy to go to Cambridge, which was then and is still now one of Britain's great universities. Late in his studies in 1666, plague swept through Europe and the universities were closed. Alone on the farm from 1666 to 1669, Newton did much of the great work of his life, including the three laws of motion, the laws of optics, the laws of universal gravitation and the mathematics behind it all, integral and differential calculus. For this, he is considered the father of modern physics.

For all his talent at theoretical work, Newton was also a practical man. He invented the reflecting telescope, the kind that you find at large observatories. He was knighted for his work at the Royal Mint, where he developed ways to catch makers of counterfeit coins.

Personally, he was very shy, and there is some speculation that he had a mild form of autism known as Asperger's Syndrome. He would rock back and forth when in intense concentration and disliked being touched. He wrote to a friend that he was proud and happy that he would die a virgin.

While his great work was finished by 1670, Newton did not like dealing with people and had to be coaxed into publishing his findings, which he finally did in 1687 in a book called the Principia Mathematica, short in Latin for the mathematical principles of physics. While the book had its detractors, soon enough the world saw how important a work it was, and Newton's became world famous.

He actually spent much more time studying the Bible and alchemy than he spent on math, but he never published these other works. Some of his religious scholarship was heretical at the time, like his proof that the Holy Trinity was physically impossible, and his calculations that the end of the world prophesized in the Bible would come in 2060 was only written in a letter to a close friend.



Leonhard Euler: born 1707, died1783: Leonhard Euler (pronounced Leonard Oiler) was born in Switzerland. His talent at math was seen at an early age and he became fast friends with the Bernoulli family, a famous few generations of Swiss scientists. He became renowned in his time as the greatest mind of his generation, and worked for both Frederich the Great of Prussia and Catherine the Great of Russia. He is a close contemporary of Ben Franklin (1706-1790), but his reputation as a scientist is much greater. He fathered 13 children, only 5 survived infancy. His first wife died and he married her sister. He went blind, but kept working until he died. In these situations, Euler has parallels with the life of the great German composer Johann Sebastian Bach (1685-1750).

His reputation during his life was very strong. The French mathematician and astronomer Pierre-Simon LaPlace wrote to his students, "Study Euler, for he is the master of us all." His place in history faded somewhat, but there was a strong comeback after all his works were finally published in a single place, 80 quarto volumes of math. (A quarto volume is about the size of a phone book.)

There are so many mathematical ideas that he pioneered, if all of them were named after him the confusion would be too great.A famous function sometimes known as the Riemann zeta function is now more accurately called the Euler-Riemann zeta function. Riemann was alive about a century later than Euler.

The base of natural logs, a very important number in calculus, is named e in honor of Euler, who did a lot of work with the number.


Carl Friedrich Gauss, born 1777, died 1855. When Gauss was born, Germany did not exist, but that is the country that now includes his home region of Brunswick. Gauss was the greatest mathematician in the first half of 19th Century. Like Newton, he wasn't rich, but the Duke of Brunswick became his mentor, and out of respect, he went to the University of Gottingen instead of the most important university in the German speaking work, the University of Berlin. Because he went there and stayed there and his best students stayed there, Gottingen became one of the top math schools in the world until it was destroyed by Nazi policies in 1933.

There is a famous story of him showing his math skills while very young. His class was being noisy, so his teacher told all the students they had to add the numbers 1 through 100 and find the sum. In less than a minute, little Carl raised his hand and gave the correct answer: 5,050.

He had his practical side as well. He is credited with inventing the telegraph and had a working model before Samuel Morse got a patent in the United States. He worked as a surveyor and an astronomer. He "re-found" the largest asteroid between Mars and Jupiter mathematically after a Sicilian astronomer found it and gave several sightings but lost it. He did it solving a difficult equation and didn't tell anyone his method. He was accused of witchcraft.

In his lifetime, Gauss' reputation was so great that when Napoleon conquered most of Europe and imposed a tax on all professors at all schools in conquered territories, the French Academy paid Gauss' tax.

Syllabus Summer 2009

Math 15: Math for Liberal Arts Summer 2009 – Laney College

Instructor: Matthew Hubbard
Text: none
Email: mhubbard@peralta.edu, profhubbard@gmail.com
website: mathlibarts.blogspot.com
Office hours:
T-Th 9:25 to 9:55 am in G-201 (math lab)
M-W 3:15-3:45 pm in G-201 (math lab)
Wednesday 6-8 (math lab)
Scientific calculator required (TI-30X IIs or TI-83 recommended)

Important academic schedule dates
Last date to add, if class is not full: Sat., June 27
Last date to drop class without a “W”: Thurs., July 2
Last date to drop class with a “W”: Wed., July 15

Holidays and professional development days that effect the Summer schedule:
None

Midterm and Finals schedule:
Thurs., July 2 Half Midterm (1 hour)
Thursday, July 9 Full Midterm (all class)
Thurs., July 23 Half Midterm (1 hour)
Thurs., July 30 (all class - comprehensive)

Grading Policy
Homework to be turned in: Assigned every Tuesday and Thursday, due the next class period
(late homework accepted AT THE BEGINNING of class period after next, 2 points off)
Quizzes: Tuesdays and Thursdays weeks without midterms – no make-up quizzes
If arranged beforehand, make-up midterms can be given, but must be taken before the next class meeting.
The two lowest scores from homework and the lowest score from quizzes will be removed from consideration before grading.

Grading system
Quizzes * 25%
Full Midterm * 25%
Two half Midterms together * 25%
Homework 20%
Final 30%

The lowest grade from Quizzes and the two Midterms will be dropped from the total.
Anyone getting a higher percentage score on the final than the weighted average of all grades combined will get the final percentage instead on the final grade, provided that student has not missed more than two homework assignments.

Academic honesty
Your homework, exams and quizzes must be your own work. Anyone caught cheating on these assignments will be punished, where the punishment can be as severe as failing the class or being put on college wide academic probation.

Class rules
Cell phones and beepers turned off, no headphones or text messaging during class
No food or drink in class, except for sealable bottles. All empty bottles should be put in the recycling bins after class is over.
You will need your own calculator and handout sheets for tests and quizzes. Do not expect to be able to borrow these from someone else.