When F = 40, C = 5/9(40-32) = 5/9(8) = 4.44 degrees
When F = 60, C = 5/9(60-32) = 5/9(28) = 15.56 degrees
When C = 30, F = 9/5(30) + 32 = 9*6 + 32 = 54 + 32 = 86 degrees
When C = 40, F = 9/5(40) + 32 = 9*8 + 32 = 72 + 32 = 104 degrees
Find where y = 7x + 4 and y = 10x - 5 intersect.
Step 1: Set the equations equal to each other and solve for x.
7x + 4 = 10x - 5_____Subtract 7x from both sides.
4 = 3x - 5_________Add 5 to both sides.
9 = 3x___________Divide both sides by 3.
3 = x
Step 2: Plug x=3 into either equation to find y.
y = 7(3) + 4 = 25
The point of intersection is (3, 25).
Kramer's rule problems.
3x + 4y = 25
4x - 2y = 4
Matrix version
[3 _4 | 25]
[4 -2 | _4]
Three matrices.
M
[3 _4 ]
[4 -2 ]
determinant = 3x(-2) - 4x4 = -6 - 16 = -22
Mx
[25 _4 ]
[ 4 -2 ]
determinant = 25x(-2) - 4x4 = -50 - 16 = -66
My
[3 _25 ]
[4 __4 ]
determinant = 3x(4) - 4x25 = 12 - 100 = -88
x = -66/-22 = 3
y = -88/-22 = 4
Answer: (3, 4)
2x + 4y = 10
4x + 8y = 30
Matrix version
[2 4 | 10]
[4 8 | 30]
Three matrices.
M
[2 4 ]
[4 8 ]
determinant = 2x8 - 4x4 = 16 - 16 = 0. This means no single solution.
Mx
[10 4 ]
[30 8 ]
determinant = 10x8 - 30x4 = 80 - 120 = -40. Since this isn't 0, the two lines are parallel.
We don't have to do the third determinant. Yay!
Answer: No solution, two parallel lines.
_x + _y = 13
3x - 3y = 9
Matrix version
[1 _1 | 13]
[3 -3 | _9]
Three matrices.
M
[1 _1 ]
[3 -3 ]
determinant = 1x(-3) - 3x1 = -3 - 3 = -6
Mx
[13 1 ]
[ 9 -3 ]
determinant = 13x(-3) - 9x1 = -39 - 9 = -48
My
[1 _13 ]
[3 __9 ]
determinant = 1x9 - 3x13 = 9 - 39 = -30
x = -48/-6 = 8
y = -30/-6 = 5
Answer: (8, 5)
Wednesday, July 29, 2009
Tuesday, July 28, 2009
Final homework not accepted late.
The last homework is due tomorrow. I will post the correct answers after class so students can study from them. I will not accept the assignment after end of class tomorrow
Monday, July 27, 2009
practice for slope and slope intercept from point slope
1a) Find the slope of the line that passes through (1, 5) and (4, -7).
1b) Find the slope intercept version of the linear equation for this line.
2a) Find the slope of the line that passes through (1, 0) and (4, 0).
2b) Find the slope intercept version of the linear equation for this line.
3a) Find the slope of the line that passes through (1, 4) and (1, -7).
3b) Find the slope intercept version of the linear equation for this line.
Answers in the comments.
1b) Find the slope intercept version of the linear equation for this line.
2a) Find the slope of the line that passes through (1, 0) and (4, 0).
2b) Find the slope intercept version of the linear equation for this line.
3a) Find the slope of the line that passes through (1, 4) and (1, -7).
3b) Find the slope intercept version of the linear equation for this line.
Answers in the comments.
Wednesday, July 22, 2009
practice for triangles, angles and sides
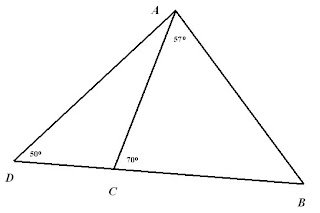In this picture, we are told the measure of three angles. This is enough information to find the measure of all the angles.1) Find the measure of angles DCA, DAC and CBA.
There is also a rule in a triangle that if one angle is larger than another, the opposite side of the big angle must be longer than the opposite side of the smaller angle.
2) Use the rule to put this list of line segments in order from longest to shortest. AB, AC, AD, BC, CD.
Answers in the comments.
Monday, July 20, 2009
Classifying triangles
There are two ways to classify triangles. The first way deals with the size of the largest angle in the triangle.
Obtuse triangle: A triangle is obtuse if the largest angle is greater than 90 degrees in measure. If the sides are given as a, b and c, where c is the longest side, if a^2 + b^2 < c^2, the triangle is obtuse.
Right triangle: If the largest angle is exactly 90 degrees in measure, the triangle is a right triangle. If the sides are given as a, b and c, where c is the longest side, a^2 + b^2 = c^2 means we have a right triangle. This is known as the Pythagorean Theorem.
Acute triangle: If the largest angle is less than 90 degrees, the triangle is called an acute triangle. If the sides are given as a, b and c, where c is the longest side, a^2 + b^2 > c^2 means we have an acute triangle.
The other method of classification has to do with having angles of the same measure or sides of the same length.
Equilateral triangle: All three angles have the same measure, 60 degrees. All three sides are the same length.
Isosceles triangle: At least two sides have the same measure, which also means two angles must have the same measure. Technically, and equilateral triangle is still isosceles, but it is a special case and we usually name it by the more specific name.
Scalene triangle: All three sides are different lengths, and all three angles are different measure.
Practice problems.
1) Can a triangle be both a right triangle and an isosceles triangle?
2) A triangle has side lengths 3, 3 and 4. What are its two classifications?
3) A triangle has two angles, 70 degrees and 15 degrees. What are its two classifications?
4) An isosceles triangle has one angle of measure 40 degrees. What are the two possible sets of angle measures and classify both as acute, right or obtuse.
5) A triangle has side lengths 5, 12 and 13. What are its two classifications?
Answers in the comments.
Obtuse triangle: A triangle is obtuse if the largest angle is greater than 90 degrees in measure. If the sides are given as a, b and c, where c is the longest side, if a^2 + b^2 < c^2, the triangle is obtuse.
Right triangle: If the largest angle is exactly 90 degrees in measure, the triangle is a right triangle. If the sides are given as a, b and c, where c is the longest side, a^2 + b^2 = c^2 means we have a right triangle. This is known as the Pythagorean Theorem.
Acute triangle: If the largest angle is less than 90 degrees, the triangle is called an acute triangle. If the sides are given as a, b and c, where c is the longest side, a^2 + b^2 > c^2 means we have an acute triangle.
The other method of classification has to do with having angles of the same measure or sides of the same length.
Equilateral triangle: All three angles have the same measure, 60 degrees. All three sides are the same length.
Isosceles triangle: At least two sides have the same measure, which also means two angles must have the same measure. Technically, and equilateral triangle is still isosceles, but it is a special case and we usually name it by the more specific name.
Scalene triangle: All three sides are different lengths, and all three angles are different measure.
Practice problems.
1) Can a triangle be both a right triangle and an isosceles triangle?
2) A triangle has side lengths 3, 3 and 4. What are its two classifications?
3) A triangle has two angles, 70 degrees and 15 degrees. What are its two classifications?
4) An isosceles triangle has one angle of measure 40 degrees. What are the two possible sets of angle measures and classify both as acute, right or obtuse.
5) A triangle has side lengths 5, 12 and 13. What are its two classifications?
Answers in the comments.
practice problems for truth tables
Instead of columns running left to right, it's easier in this text editor to make a truth table that is put together in rows going from top to bottom
Here is an example: Create the truth table for (p OR q) IMPLIES q.
p__________________ T T F F
q__________________ T F T F
p OR q_____________ T T T F
(p OR q) IMPLIES q_ T F T T
Not a tautology, because of the F in the second position.
Try the following.
a) (p IMPLIES q) OR (p IMPLIES NOT q)
b) (NOT p) IMPLIES (p IMPLIES q)
Answers in the comments.
Here is an example: Create the truth table for (p OR q) IMPLIES q.
p__________________ T T F F
q__________________ T F T F
p OR q_____________ T T T F
(p OR q) IMPLIES q_ T F T T
Not a tautology, because of the F in the second position.
Try the following.
a) (p IMPLIES q) OR (p IMPLIES NOT q)
b) (NOT p) IMPLIES (p IMPLIES q)
Answers in the comments.
Wednesday, July 15, 2009
practice for bitwise operators
p = 1001 1010
q = 0110 0110
r = 1011 0001
^ means and
v means or
~ means not
Order of operations: parentheses first, otherwise left to right
Find the following values.
a) p v q
b) p ^ r
c) p v ~q
d) ~p v q
e) r ^ ~q
f) ~(r ^ q)
Answers in the comments.
q = 0110 0110
r = 1011 0001
^ means and
v means or
~ means not
Order of operations: parentheses first, otherwise left to right
Find the following values.
a) p v q
b) p ^ r
c) p v ~q
d) ~p v q
e) r ^ ~q
f) ~(r ^ q)
Answers in the comments.
Sunday, July 12, 2009
Five computer scientists
Here are the highlights of the life stories of five important people in the history of computer science. There are many others, but these folks made significant contributions and their lives have interesting and unique tidbits which will be shared here.
Born Janos Von Neumann in Hungary, he is known to posterity as John Von Neumann, though his friends always called him Johnny.
I give Von Neumann the first position on this list because he is the greatest mathematician on the list. The list of four great mathematicians I lectured about on the first day only takes us through to 1855, when Gauss dies. If we were listing great mathematicians since then, almost all mathematicians would put Bernhard Riemann, Henri Poincaré, David Hilbert and John Von Neumann on the list of the greatest of the great.
Not Albert Einstein. He is a great physicist, but not a great mathematician.
Von Neumann started his career in chemistry, but after he did the mathematical groundwork for the ideas of quantum mechanics, he switched to mathematics. This is some of the strangest and least intuitive mathematics ever done, and it shows that at the sub-atomic level, it is possible for some small objects to be in two places at the same time. When people would ask him how he understood some of the strange ideas he came up with in his life, Von Neumann said: "You don't really ever understand higher mathematics. You just get used to it."
Besides his work in mathematical physics, Von Neumann solved a conjecture of Borel and created the field now known as game theory. A century before, a Prussian tactician named Von Clausewitz put forward the idea of total war, that a country at war must put forward every available resource or it wasn't truly war at all. Von Neumann's game theory proved Von Clausewitz wrong, that successful war strategies include bluffs and strategic ways to put forward only part of the available resources and still meet your objectives.
Among his practical inventions include the trigger for the hydrogen bomb, which makes an atomic explosion "slow" enough that it begins a larger chain reaction instead of obliterating all matter in a radius of several hundred yards instantly. The larger chain reaction makes for an explosion thousands to millions of times stronger.
The reason Von Neumann is on this list is because he invented the idea of software. When the first computer were created, they had to be re-wired by hand every time a new problem was to be solved. There was computer memory, but it just stored data. Von Neumann put forward the idea that some of the memory hold instructions, and the computer should be hard-wired to understand these instructions. It is nearly impossible to overestimate the importance of this idea.
Von Neumann died of cancer in 1957 at the age of 53. The amount of important work he did in such a short life is as amazing as any of the great composers who died young, like Mozart or Chopin.
Alan Turing was born in England, and he was an excellent math student before the innovation of computers. He is given credit as one of the people who proved the Central Limit Theorem, a key fact that makes statistics work.
Turing's most famous practical work was breaking the German codes during World War II using some of the first computers ever built. The Germans had a code machine called Enigma, which could scramble a message in a way that was very difficult to unscramble without another Enigma machine at the other end AND the particular starting position of the machine when the operator began typing the message in. The British code breaking team was housed during the war at Bletchley Park, and some of the things that happened there have only been de-classified in the past ten years of so. All the information points to Turing as being the intellectual star of the team.
Turing also came up with theoretical concepts in early computers, including the Turing machine, an idealized computer with two tapes, one for input and one for output, and the Turing test for artificial intelligence.
Turing was also very openly gay at a time when that was illegal. He was charged in a court of law with engaging in homosexual acts and found guilty. He was given the option of going to jail or taking a "cure" of estrogen treatments. He chose the cure. It did nothing to change his feelings, but it did make his breasts bigger.
Turing died in 1954 at the age of 41 from eating a poison apple. He was working on electrolysis, a way of plating one metal on top of another, in this case silver plating, and absent-mindedly picked up an apple and took a bite when his hands were covered with poisonous chemicals. The authorities ruled it a suicide, though Turing's mother believed it was just an accident.
Back in the day, the actual work of programming was considered "woman's work", and many of the programmers back in the era of the huge mainframes were women, who were considered better suited to the painstaking work of making sure there were no errors in a piece of computer code. This stereotype made it possible for some women to get employment other than secretarial work in business in the middle of the century in the United States, and the stereotype continued in Japan well into the 1980's, when I was a programmer of video games in the U.S. In the era of Pac-Man and Donkey Kong, the video game designers in Japan were men, but the programmers were women.
Grace Hopper was born in New York City in 1906. She was a good math student, getting her bachelor's degree from Vassar and her doctorate at Yale. During World War II, she worked for the Navy and was on the team creating some of the first computers used by the U.S. Military, including the Mark I.
She is given credit for finding the first computer bug, which means a mistake in the program which keeps it from running properly. The bug she found was an actual bug, a moth that found its way into the computer and died when it hit the exposed wires, causing a short circuit.
Her ideas about designing a software language gave rise to COBOL, a language that was the standard for business software for many decades. Though it has been eclipsed by more modern languages, there are still listings for jobs for people who program in COBOL to this day.
She wanted to understand the connection between the speed of light and the workings of the computer that work on electricity, which moves at very close to the speed of light, so she had engineers cut pieces of wire that would show how far electricity would travel in a nanosecond, a billionth of a second, and she would hand these wires out when she gave lectures.
Hopper kept her Navy commission throughout her life, and retired with the rank of Rear Admiral.
She died in 1992 at the age of 85. She was buried with full military honors at Arlington National Cemetery. The U.S.S Hopper is one of the few ships in the Navy named after a woman, and the ship has the same nickname that the admiral had in life, Amazing Grace.
Edsger Dijkstra was born in Holland in 1930, about a generation after Hopper and Turing and Von Neumann, and his contributions to computer science dealt with changing computer programming from a haphazard practice to a well-structured and defined set of proper practices.
He started working in computers in the 1950's, and computers were still strange and exotic devices to the general public. When Dijkstra applied for his wedding license, her put "computer programmer" down as his line of work. The clerk at the registrar's office made him change it, saying that nobody programmed computers for a living. He crossed it out and wrote "theoretical physicist", which the registrar accepted as a real job people get paid for.
While Dijkstra is given credit for developing some important methods for solving problems, his main influence today is the idea that a computer program should be completely designed before anyone ever starts typing in code into a machine. There were some computer languages he felt caused people to fall into bad habits, including Grace Hopper's COBOL and other popular languages of the 1960's, including BASIC and FORTRAN. A more modern concept in programming called object oriented programming also met with his disapproval. "Object oriented programming is an exceptionally bad idea that could only have originated in California."
Another famous quote attributed to him is: "Computer Science is no more about computers than astronomy is about telescopes."
Dykstra died at the age of 72 in 2002. When asked by an interviewer what he would like to be remembered for, he replied: "If some day, someone is writing a computer program and is thinking about how to do a quick and sloppy job, and for a moment that person considers 'What would Dykstra make of this?', then decides to design the program carefully, that will be immortality enough for me."
Donald Knuth was born in Wisconsin in 1938. He was a very good student and at an early age he showed how obsessed he could be with solving a problem. He skipped nearly a week from high school trying to win a national competition to find the most words that could be made using the letters in the phrase "Ziegler's Giant Bar." Knuth found 2,500 words. The second place competitor found about 600. He said he could have found more if he had realized he was allowed to use the apostrophe. The prize was a television set, which he donated to the high school.
Knuth's best known work is the textbook series The Art of Computer Programming. The first four volumes have been around since the 1970s and 1980s. The fifth volume was released only a few years back. When people send Knuth corrections to his textbooks, he send the first person who correctly spots an error a check for $2.56. The number 256 is the number of different patterns an eight bit binary string can create. Most people who get the checks frame them and hang them on their walls as souvenirs.
Donald Knuth is still alive and is professor emeritus of computer science at Stanford University. A devout Lutheran, his web page lists his public speaking engagements, and includes the Sundays when he will give a sermon as the deacon of his church on some text from the Bible.
Born Janos Von Neumann in Hungary, he is known to posterity as John Von Neumann, though his friends always called him Johnny.
I give Von Neumann the first position on this list because he is the greatest mathematician on the list. The list of four great mathematicians I lectured about on the first day only takes us through to 1855, when Gauss dies. If we were listing great mathematicians since then, almost all mathematicians would put Bernhard Riemann, Henri Poincaré, David Hilbert and John Von Neumann on the list of the greatest of the great.
Not Albert Einstein. He is a great physicist, but not a great mathematician.
Von Neumann started his career in chemistry, but after he did the mathematical groundwork for the ideas of quantum mechanics, he switched to mathematics. This is some of the strangest and least intuitive mathematics ever done, and it shows that at the sub-atomic level, it is possible for some small objects to be in two places at the same time. When people would ask him how he understood some of the strange ideas he came up with in his life, Von Neumann said: "You don't really ever understand higher mathematics. You just get used to it."
Besides his work in mathematical physics, Von Neumann solved a conjecture of Borel and created the field now known as game theory. A century before, a Prussian tactician named Von Clausewitz put forward the idea of total war, that a country at war must put forward every available resource or it wasn't truly war at all. Von Neumann's game theory proved Von Clausewitz wrong, that successful war strategies include bluffs and strategic ways to put forward only part of the available resources and still meet your objectives.
Among his practical inventions include the trigger for the hydrogen bomb, which makes an atomic explosion "slow" enough that it begins a larger chain reaction instead of obliterating all matter in a radius of several hundred yards instantly. The larger chain reaction makes for an explosion thousands to millions of times stronger.
The reason Von Neumann is on this list is because he invented the idea of software. When the first computer were created, they had to be re-wired by hand every time a new problem was to be solved. There was computer memory, but it just stored data. Von Neumann put forward the idea that some of the memory hold instructions, and the computer should be hard-wired to understand these instructions. It is nearly impossible to overestimate the importance of this idea.
Von Neumann died of cancer in 1957 at the age of 53. The amount of important work he did in such a short life is as amazing as any of the great composers who died young, like Mozart or Chopin.
Alan Turing was born in England, and he was an excellent math student before the innovation of computers. He is given credit as one of the people who proved the Central Limit Theorem, a key fact that makes statistics work.
Turing's most famous practical work was breaking the German codes during World War II using some of the first computers ever built. The Germans had a code machine called Enigma, which could scramble a message in a way that was very difficult to unscramble without another Enigma machine at the other end AND the particular starting position of the machine when the operator began typing the message in. The British code breaking team was housed during the war at Bletchley Park, and some of the things that happened there have only been de-classified in the past ten years of so. All the information points to Turing as being the intellectual star of the team.
Turing also came up with theoretical concepts in early computers, including the Turing machine, an idealized computer with two tapes, one for input and one for output, and the Turing test for artificial intelligence.
Turing was also very openly gay at a time when that was illegal. He was charged in a court of law with engaging in homosexual acts and found guilty. He was given the option of going to jail or taking a "cure" of estrogen treatments. He chose the cure. It did nothing to change his feelings, but it did make his breasts bigger.
Turing died in 1954 at the age of 41 from eating a poison apple. He was working on electrolysis, a way of plating one metal on top of another, in this case silver plating, and absent-mindedly picked up an apple and took a bite when his hands were covered with poisonous chemicals. The authorities ruled it a suicide, though Turing's mother believed it was just an accident.
Back in the day, the actual work of programming was considered "woman's work", and many of the programmers back in the era of the huge mainframes were women, who were considered better suited to the painstaking work of making sure there were no errors in a piece of computer code. This stereotype made it possible for some women to get employment other than secretarial work in business in the middle of the century in the United States, and the stereotype continued in Japan well into the 1980's, when I was a programmer of video games in the U.S. In the era of Pac-Man and Donkey Kong, the video game designers in Japan were men, but the programmers were women.
Grace Hopper was born in New York City in 1906. She was a good math student, getting her bachelor's degree from Vassar and her doctorate at Yale. During World War II, she worked for the Navy and was on the team creating some of the first computers used by the U.S. Military, including the Mark I.
She is given credit for finding the first computer bug, which means a mistake in the program which keeps it from running properly. The bug she found was an actual bug, a moth that found its way into the computer and died when it hit the exposed wires, causing a short circuit.
Her ideas about designing a software language gave rise to COBOL, a language that was the standard for business software for many decades. Though it has been eclipsed by more modern languages, there are still listings for jobs for people who program in COBOL to this day.
She wanted to understand the connection between the speed of light and the workings of the computer that work on electricity, which moves at very close to the speed of light, so she had engineers cut pieces of wire that would show how far electricity would travel in a nanosecond, a billionth of a second, and she would hand these wires out when she gave lectures.
Hopper kept her Navy commission throughout her life, and retired with the rank of Rear Admiral.
She died in 1992 at the age of 85. She was buried with full military honors at Arlington National Cemetery. The U.S.S Hopper is one of the few ships in the Navy named after a woman, and the ship has the same nickname that the admiral had in life, Amazing Grace.
Edsger Dijkstra was born in Holland in 1930, about a generation after Hopper and Turing and Von Neumann, and his contributions to computer science dealt with changing computer programming from a haphazard practice to a well-structured and defined set of proper practices.
He started working in computers in the 1950's, and computers were still strange and exotic devices to the general public. When Dijkstra applied for his wedding license, her put "computer programmer" down as his line of work. The clerk at the registrar's office made him change it, saying that nobody programmed computers for a living. He crossed it out and wrote "theoretical physicist", which the registrar accepted as a real job people get paid for.
While Dijkstra is given credit for developing some important methods for solving problems, his main influence today is the idea that a computer program should be completely designed before anyone ever starts typing in code into a machine. There were some computer languages he felt caused people to fall into bad habits, including Grace Hopper's COBOL and other popular languages of the 1960's, including BASIC and FORTRAN. A more modern concept in programming called object oriented programming also met with his disapproval. "Object oriented programming is an exceptionally bad idea that could only have originated in California."
Another famous quote attributed to him is: "Computer Science is no more about computers than astronomy is about telescopes."
Dykstra died at the age of 72 in 2002. When asked by an interviewer what he would like to be remembered for, he replied: "If some day, someone is writing a computer program and is thinking about how to do a quick and sloppy job, and for a moment that person considers 'What would Dykstra make of this?', then decides to design the program carefully, that will be immortality enough for me."
Donald Knuth was born in Wisconsin in 1938. He was a very good student and at an early age he showed how obsessed he could be with solving a problem. He skipped nearly a week from high school trying to win a national competition to find the most words that could be made using the letters in the phrase "Ziegler's Giant Bar." Knuth found 2,500 words. The second place competitor found about 600. He said he could have found more if he had realized he was allowed to use the apostrophe. The prize was a television set, which he donated to the high school.
Knuth's best known work is the textbook series The Art of Computer Programming. The first four volumes have been around since the 1970s and 1980s. The fifth volume was released only a few years back. When people send Knuth corrections to his textbooks, he send the first person who correctly spots an error a check for $2.56. The number 256 is the number of different patterns an eight bit binary string can create. Most people who get the checks frame them and hang them on their walls as souvenirs.
Donald Knuth is still alive and is professor emeritus of computer science at Stanford University. A devout Lutheran, his web page lists his public speaking engagements, and includes the Sundays when he will give a sermon as the deacon of his church on some text from the Bible.
Wednesday, July 8, 2009
Practice for tomorrow's exam
Consider the contingency table below. The columns represent A and A-bar, the complement of A, while the rows represent B and its complement B-bar. The numbers are the number of element in each intersection.
_______________A____A-bar_____row totals
B_____________25________________75
B-bar_________________50___________
col. totals___90_____________________grand total
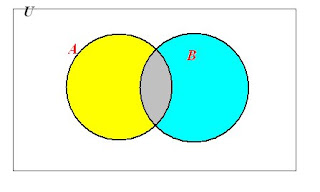Use the numbers from the filled in table to find the cardinalities in each section.
Cardinality in white section =
Cardinality in yellow section =
Cardinality in gray section =
Cardinality in cyan section =
Answers in the comments.
_______________A____A-bar_____row totals
B_____________25________________75
B-bar_________________50___________
col. totals___90_____________________grand total
Use the numbers from the filled in table to find the cardinalities in each section.Cardinality in white section =
Cardinality in yellow section =
Cardinality in gray section =
Cardinality in cyan section =
Answers in the comments.
Practice with Polish notation
Find the values of the numbers from these expressions.
- + ^ 10 2 20 + 12 17 =
- 12 * 2 + 4 ^ 3 - 2 1 =
Turn these equations in standard notation into Polish notation.
y = ax^2 + bx + c
A = Pe^(rt)
Answers in the comments.
- + ^ 10 2 20 + 12 17 =
- 12 * 2 + 4 ^ 3 - 2 1 =
Turn these equations in standard notation into Polish notation.
y = ax^2 + bx + c
A = Pe^(rt)
Answers in the comments.
Tuesday, July 7, 2009
Practice for test 7/7
A) A rock concert registers at about 105 decibels and a jet engine at 140 decibels. How many more times the energy is produced by the engine compared to the speakers at the concert?
Use the order of operations to get a single number from these mathematical terms. If the answer is not a whole number, round to two places after the decimal.
Note: sqrt(...) means square root, / means division, ^ means exponentiation and * mean multiplication.
B) sqrt(7^2 + 1^2)
C) 8 - 4
__12-(-8)
D) 3(5+2) - 4/6*15 + 8(3/2)
Answers in the comments.
Use the order of operations to get a single number from these mathematical terms. If the answer is not a whole number, round to two places after the decimal.
Note: sqrt(...) means square root, / means division, ^ means exponentiation and * mean multiplication.
B) sqrt(7^2 + 1^2)
C) 8 - 4
__12-(-8)
D) 3(5+2) - 4/6*15 + 8(3/2)
Answers in the comments.
Friday, July 3, 2009
Practice problems for homework due July 6
"^" means exponentiation. "sqrt(x)" means square root of x, which can also be written as "x^(1/2)". The symbol ~= means approximately equal.
log 5 ~= .69897 and log 7 ~= .84510.
log(a*b) = log a + log b
log(a/b) = log a - log b
log a^b = b*log a
log (sqrt(a)) = 1/2*log a.
Find the following values, rounded to the nearest five decimals.
a) log 35 =
b) log (sqrt(35)) =
c) log 7/5 =
The prime factorization of 108 is 2^2 * 3^3. Find the simplified radical form of for the following radicals, and the approximations to five significant digits.
d) sqrt(108) =
e) 108^(1/3) =
f) An earthquake registering 5.7 is recorded one morning, and in the afternoon, another quake 27 times stronger is felt. Give the Richter reading of the second stronger quake. (Nearest tenth.)
g) What is the decibel reading of a sound that is 7 times louder than a 75 decibel reading. (Nearest decibel.)
Answers in the comments.
log 5 ~= .69897 and log 7 ~= .84510.
log(a*b) = log a + log b
log(a/b) = log a - log b
log a^b = b*log a
log (sqrt(a)) = 1/2*log a.
Find the following values, rounded to the nearest five decimals.
a) log 35 =
b) log (sqrt(35)) =
c) log 7/5 =
The prime factorization of 108 is 2^2 * 3^3. Find the simplified radical form of for the following radicals, and the approximations to five significant digits.
d) sqrt(108) =
e) 108^(1/3) =
f) An earthquake registering 5.7 is recorded one morning, and in the afternoon, another quake 27 times stronger is felt. Give the Richter reading of the second stronger quake. (Nearest tenth.)
g) What is the decibel reading of a sound that is 7 times louder than a 75 decibel reading. (Nearest decibel.)
Answers in the comments.
Wednesday, July 1, 2009
Practice problems for the test on 7/2
The Transformers sequel made $108,966,307 this weekend.
a) Round this number to one significant digit.
b) Round this number to two significant digits.
c) Round this number to three significant digits.
According to the calculator 50! rounds to 3.041 x 10^64 and 60! rounds to 8.321 x 10^81, both rounded to four significant digits. Find the following values.
d) 50! / 60!
e) 60! / 50!
f) 50! x 60!
(note: the calculator will tell you overflow error on problem f because it doesn't like numbers bigger than 10^100 power. You will have to do this one by hand.)
Answers in the comments.
a) Round this number to one significant digit.
b) Round this number to two significant digits.
c) Round this number to three significant digits.
According to the calculator 50! rounds to 3.041 x 10^64 and 60! rounds to 8.321 x 10^81, both rounded to four significant digits. Find the following values.
d) 50! / 60!
e) 60! / 50!
f) 50! x 60!
(note: the calculator will tell you overflow error on problem f because it doesn't like numbers bigger than 10^100 power. You will have to do this one by hand.)
Answers in the comments.
Subscribe to:
Posts (Atom)
